数据恢复基础 - 7."数" 之体验
|
1.3 "数" 之体验 数据恢复的过程,也就是一个与数打交道的过程。在此,我们有必要先介绍一些有关数的基础知识。
1.3.1 数制
数制,也就是我们常说的二进制、八进制、十进制、十六进制等。在数据恢复过程中,经常会遇到数的不同表现形式。因为计算机使用二进制,我们使用磁盘编辑软件时看到的是十六进制,而我们最习惯的则是十进制。在此,我们对各种数制做一个简单的介绍。
1)十进制
在我们的日常生活中,数的表示方法为“十进制”,也就是逢十进位,10进制使用十个阿拉伯数字:0、1、2、3、4、5、6、7、8、9。十进制使用后缀d表示,但一般情况下会省略掉。
2)二进制
对于计算机来说,它能识别的只有“0”和“1”,这就是“二进制”,逢二进位。二进制只使用0和1两个数字,每个0或者1称为一个“位(bit)”,每8个“bit”组成一个“字节(byte)”。二进制使用后缀b表示,如110b。
但是在实际应用中,二进制的书写长度是一个非常令人头痛的事情,因此又引入了八进制和十六进制。因为进制越大,数的表达长度也就越短。而之所以使用“八进制”和“十六进制”,是因为“8”和“16”分别是“2的3次方”和“2的4次方”,这就使得这三种进制之间的转换非常直接。八进制或十六进制缩短了二进制数,同时又保持了二进制数的表达特点。在数据恢复的实际工作当中,我们常用到的是十六进制,所以在此只介绍十六进制,而不再介绍八进制。
3) 十六进制
十六进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A、B、C、D、E、F(字母不区分大小写)这六个字母来分别表示10、11、12、13、14、15。也就是说,十六进制使用0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F这十六个数字。十六进制使用后缀H表示,如872H表示这是一个十六进制数,也可以表示成0x872,在本书中,我们采用后一种表示方式。
1.3.2 数制间的转换
只了解数制还不够,因为在实际应用中还经常需要在它们之间进行相应的转换,现在我们就来介绍一下数制间的相互转换方法。
1)二进制转换为十进制
在介绍二进制转换为十进制之前,我们先来了解一下二进制的“位权”,如表1.1所示。
表1.1 二进制的位权
可以看到,第N位的位权也就是2的N-1次幂。在将二进制换算成十进制时,就是用每位的数值乘以它的位权,然后将所有的乘积相加。如:
10101011 b = 1×20 + 1×21 + 0×22 + 1×23 + 0×24 + 1×25 + 0×26 + 1×27 = 171
2)十六进制转换为十进制
十六进制转换成十进制时,原理与二进制转换成十进制相同,只是将底数换成16即可。需要注意的是,在十六进制中,10~15依次用A、B、C、D、E、F表示,在遇到A~F字符时,运算过程中需要将该字符替换成它所表达的对应的数字。
假设有一个十六进制数0x2AF5,转换成十进制时,方法为:
5 × 160 + F × 161 + A × 162 + 2 × 163 = 10997
3)十进制转换为二进制
十进制转换为二进制时,将十进制数除以2,得到商和余数;然后再用商作为被除数除以2,得到商与余数;再用商作为被除数除以2……直到商为0。然后将每次相除时的余数倒序排列,即得到转换后的二进制。如图1.8所示,6转换成二进制后为110b。
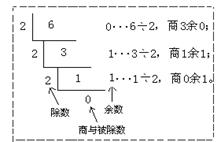 图1.8 十进制转换成二进制
4)十进制转换为十六进制
十进制转换成十六进制时,与转换成二进制的方法相同,只是将除数2换成16即可。例如,将130转换成十六进制:
130 / 16 = 8 余 2
8 / 16 = 0 余 8
即,130转换成十六进制的结果为0x82。
5)二进制、十六进制间的相互转换
二进制和十六进制的互相转换比较重要,它们之间的转换非常的方便:将二进制数从右向左每四位分为一段,最后一段如果不足四位,在其左边补0;然后将各段分别转换成十六进制即可。例如,将110101100101001101b转换为十六进制时,如表1.2所示。
表1.2 将110101100101001101b转换成十六进制
所以,110101100101001101b转换成十六进制后的值为0x3594D。
1.3.3 取整与取余运算
取整运算是指在进行除法运算时,只取商作为结果,余数部分则舍弃。取整运算符为“DIV”,例如:
512 DIV 510 = 1
取余运算是指在进行除法运算时,只取余数作为结果,将商舍弃。取余运算符为“MOD”,例如:
512 MOD 510 = 2
1.3.4 数的存储格式
数的存储格式,也就是数字的存储顺序。在表示数值的大小时,一个字节(Byte)最大只能表示到255(0xFF),这是远远不够的。为了满足实际使用的需要,通常会使用2个、4个、或者8个字节(Byte)来表示数值的大小。对于使用多字节表示数值的情况,就存在一个顺序问题。数的存储顺序有两种——Big-endian格式和Little-endian格式。
例如,有一个十六进制数“23 48 BA 4C”,使用Big-endian格式存储形式为“23 48 BA 4C”;而使用Little-endian格式的文件系统中,存放的形式则是“4C BA 48 23”,即低位在前,高位在后。

|

